Omnitruncated 5-cell honeycomb
| Omnitruncated 4-simplex honeycomb | |
|---|---|
| (No image) | |
| Type | Uniform honeycomb |
| Family | Omnitruncated simplectic honeycomb |
| Schläfli symbol | t0,1,2,3,4{3[5]} |
| Coxeter–Dynkin diagrams | |
| 4-face types | t0,1,2,3{3,3,3} |
| Cell types | t0,1,2{3,3} {6}x{} |
| Face types | {4} {6} |
| Vertex figure | Irr. 5-cell |
| Coxeter groups | 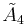 , [3[5]] , [3[5]] |
| Properties | vertex-transitive, cell-transitive |
In four-dimensional Euclidean geometry, the omnitruncated 4-simplex honeycomb or omnitruncated 5-cell honeycomb is a space-filling tessellation honeycomb. It is composed entirely of omnitruncated 5-cell (omnitruncated 4-simplex) facets.
Coxeter calls this Hinton's honeycomb after C. H. Hinton, who described it in his book The Fourth Dimension in 1906.[1]
Contents |
Alernate names
- Omnitruncated cyclopentachoric tetracomb
- Great-prismatodecachoric tetracomb
Related polytopes and honeycombs
This honeycomb is one of 7 unique uniform honycombs constructed by the 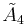 Coxeter group. The Coxeter–Dynkin diagrams of the other six are: , , , , ,.
Coxeter group. The Coxeter–Dynkin diagrams of the other six are: , , , , ,.
See also
- Regular and uniform honeycombs in 4-space:
Notes
References
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings)
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs) Model 140
- Richard Klitzing, 4D, Euclidean tesselations, x3x3x3x3x3*a - otcypit - 140